|
|
Prof. Dr. Arnaldo Gammal
 |
|
Área de Pesquisa: Átomos Ultrafrios,
Condensados de Bose-Einstein
Em 1924, S.N. Bose rederivou a fórmula de Planck para a radiação de corpo
negro usando uma hipótese de que os fótons são indistingüíveis, gerando
assim uma nova maneira de fazer a estatística de distribuição de energia.
No mesmo ano, Einstein aplicou essa estatística de Bose a um gás e previu
que para baixíssimas temperaturas deveria haver um enorme adensamento dos
átomos no nível de energia mais baixo, o que passou se chamar de
condensado de Bose-Einstein. Condensados atômicos foram realizados
experimentalmente em 1995 pelos laboratórios do JILA (Boulder-Colorado),
Rice (Houston-TX) e MIT (Boston), resfriando gases de rubídio, lítio e
sódio respectivamente, chegando em temperaturas da ordem de nano-Kelvin .
Isso deu enorme impulso para pesquisa teórica e experimental nessa área
com grandes promessas tecnólogicas. A longo prazo, acredita-se que essa
área possa contribuir para instrumentos de altíssima precisão, navegação,
litografia, computação quântica e supercondutividade.
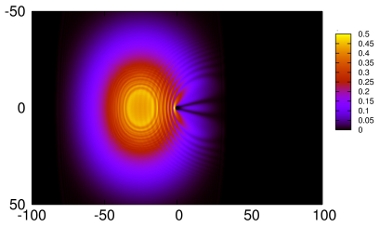
Nossa pesquisa presente envolve a compreensão de como evoluem os
condensados atômicos no tempo e determinação de estados fundamentais do
sistema. Um condensado diluído e com fraca interação interatômica pode
ser descrito numa aproximação de campo médio. Esta aproximação resulta em
uma equação de Schrödinger com um termo não linear que descreve a
interação entre os átomos e é chamada de equação de Gross-Pitaevskii.
Assim, o condensado pode ser considerado um laboratório
de física não linear, com a presença de fenômenos como difração não
linear, colapso, sólitons, vórtices e ondas de choque. Condensados também
permitem estudos de sistemas de física da matéria condensada em situações
controladas onde diversos parâmetros podem ser modificados. Para estudo
da evolução temporal construímos diversos códigos computacionais para
solução de equações diferenciais parciais. Esses trabalhos vem sendo
desenvolvidos com a participação de alunos e colaboradores (veja na lista
de publicações).
Também temos interesse em estudos que vão além do campo médio usando
métodos de Monte-Carlo e multi-orbitais.
Vagas abertas: Iniciação, Mestrado e Doutorado.
OPEN POSITIONS: PhD, Post-doc
Acessos:  |
last modified
Sept 19th, 2022
|
|
|

