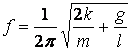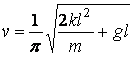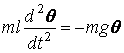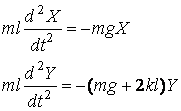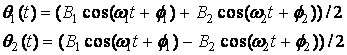Alguma física do andar

Velocidade do andar

O ato de andar (de um bípede, como uma pessoa, por exemplo) pode parecer bastante complicado se o analisamos de um referencial fixo ao solo: as pernas vão sempre para a frente, com velocidade variável; durante algum tempo o pé se desloca, com velocidade mais alta que a média da velocidade da pessoa e, ao tocar o solo, para; quando o pé está parado em relação ao solo, a perna faz um movimento para a frente, como que rodando em torno dele; além disso tudo, as pernas se dobram ligeiramente quando andamos Parece, então, que o andar é um movimento bastante complicado para se analisar fisicamente. Entretanto...

Às vezes, olhar um mesmo problema físico de um outro ponto de vista pode facilitar o seu entendimento. Por exemplo, o ato de andar pode ser descrito fisicamente de forma muito simples se analisamos movimento de um referencial que se move com a mesma velocidade de quem anda. Neste caso vemos o corpo parado e as pernas oscilando para frente e para trás, alternadamente.

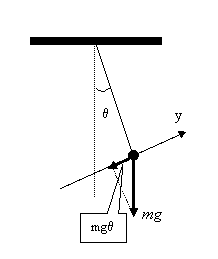
Outra tática usualmente adotada em física é procurar o que um problema tem de mais essencial para simplificá-lo, deixando os detalhes complicadores para depois. Assim, podemos ignorar o fato da perna se dobrar um pouco a cada passo e considerá-la como um pêndulo. Mais ainda, podemos considerar a perna com um pêndulo simples, como se houvesse uma massa pendurada na ponta de um fio bem leve.

Olhando então o movimento do andar de um referencial que se desloca com a pessoa, vemos o seu corpo parado e ar pernas pendulando livremente. Podemos concluir, então, que a forma mais confortável de andar é aquela em que as pernas, olhada desse referencial que se desloca com a pessoa, oscilam com suas freqüências próprias, pois assim não se gasta energia para acelerá-las ou freá-las.

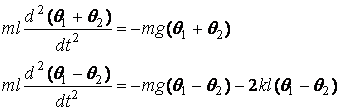
Se aproximarmos uma perna humana por um pêndulo simples[1], de comprimento l, vemos que, em um andar confortável, elas oscilam com período de

. (1)

A velocidade do andar pode ser calculada considerando então o tamanho de um passo. Se a abertura da perna for da ordem de 30º, o tamanho de um passo será de aproximadamente l/2. Como em um período completo de oscilação damos dois passos, a velocidade confortável de andar é de aproximadamente

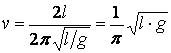. (2)

Para um adulto, o comprimento da perna é da ordem de 1 m. Assim, a velocidade confortável de andar é da ordem de 1,0 m/s, ou 3,6 km/h, velocidades bem típicas para seres humanos.

Adultos, crianças e ... outros animais

Um aspecto interessante da equação 2 é que a velocidade do andar confortável depende da raiz quadrada do comprimento da perna. Isso pode explicar porque adultos e crianças, cuja relação de tamanho é da ordem de 2, podem andar lado-a-lado sem grandes esforços: a relação entre as velocidades confortáveis do andar é de e, portanto, basta que o adulto encurte seus passos de uns 15% ou 20% e a criança aumente seus passos também de uns 15% ou 20% para que ambos consigam andar confortavelmente.

O modelo do andar com pernas oscilantes não deve ser bom para todos os animais, especialmente para aqueles muito pequenos, pois o atrito com o ar e o atrito interno podem não ser desprezíveis. Os mecanismos de “grudar” os pés onde anda (para andar de ponta-cabeça, como no caso de uma formiga no teto) também podem mudar muito a situação. Mas o modelo deve valer para animais pequenos como um cachorro ou um gato e grandes como uma girafa ou um elefante. Assim, embora esses grandes animais possam ter pernas dez vezes maiores que os pequenos, suas velocidades naturais de andar mantém uma relação de velocidades de aproximadamente 3 para 1. Se você tiver dúvidas, uma ida ao zoológico pode esclarecer.

Física interplanetária

Um outro aspecto interessante da equação (2) é a dependência da velocidade do andar com a aceleração da gravidade, : um mesmo animal anda mais rápido em um planeta onde a aceleração gravitacional é maior e mais devagar onde ela é menor. Talvez isso explique porque astronautas “andando” na Lua acabavam, na verdade, por correr: desabituado com a nova realidade gravitacional, o cérebro de uma pessoa na Lua quer atingir um determinado ponto no mesmo tempo que ele o atingiria se estivesse na Terra; quer também que sua perna vá para frente tão rapidamente quanto estava acostumado aqui na Terra. Como conseqüência, acaba, na verdade, “correndo”, ou seja, levantava o pé que estava atrás antes do pé da frente tocar o solo.

Assim como a capa do super-herói balança quando ele viaja entre as estrelas, apesar da ausência de ar, presumo que os viajantes interplanetários dos filmes de fantasia caminhem nos diferentes planetas com velocidades independentes das acelerações gravitacionais locais.

Quer andar mais rápido? Amarre as pernas.

O título acima é meio paradoxal, mas é isso mesmo. Se você quiser andar de forma confortável – sem fazer esforços para acelerar e parar a perna a cada passo, como fazemos normalmente para andar rápido – amarre as pernas. Mas, amarre com elásticos.

A freqüência natural de oscilação de um pêndulo depende da força de restauração que o puxa para o ponto de equilíbrio, o ponto mais baixo, quando ele é deslocado. Assim, se aumentarmos essa força de restauração, que é apenas a força gravitacional em um situação usual, podemos aumentar a freqüência natural de um pêndulo. Para aumentar a força de restauração basta ligar os dois pés com um elástico ou uma mola. Por exemplo, se os dois pés são ligados por um elástico que provoque uma força de restauração igual a k×x, onde x é a distância entre os dois pés, então a freqüência natural de oscilação (continuamos considerando as pernas como pêndulos simples) será

, (3)

onde m é a massa da perna. (A dedução dessa expressão está feita na próxima seção. Ela é um pouco elaborada e depende de alguma familiaridade com as técnicas de cálculo estudadas nos primeiros anos dos cursos de física, matemática ou engenharia.)

Se o tamanho do passo não é alterado, então a velocidade do andar confortável, aquele em que as pernas oscilam naturalmente, é

. (4)

Como k é um número positivo, então essa velocidade confortável de andar – com as pernas amarradas – é maior do que aquela da equação 2.

Dedução da equação 3

Considere inicialmente um pêndulo simples, uma massa m pendurada em um fio de comprimento l (veja a figura abaixo). Se esse pêndulo é deslocado da posição de equilíbrio, então surge uma força que o empurra de volta para aquela posição. Essa força é dada pela componente da força peso, mg, ao longo de uma direção perpendicular à direção do pêndulo, ou seja, mg×sen(q). Se o ângulo q é pequeno (o que corresponde a pequenas oscilações em torno da posição de equilíbrio), podemos aproximar sen(q) por q. Assim, a segunda lei de Newton para o pêndulo fica

, (5)

onde y é aquele eixo “torto” da figura, perpendicular à direção do pêndulo, e o sinal menos é porque a força é na direção oposta a y. Mas se q é pequeno, podemos aproximar y por lq. Assim, a equação (5) fica

. (6)

A solução dessa equação é

, (7)

onde A é a amplitude de oscilação,

(8)

e é um ângulo que depende da situação em t=0. Mas o que importa para saber com que freqüência o pêndulo oscilará é apenas o valor de w e não precisamos nos ocupar com A e .

Considere agora dois pêndulos simples de comprimento l e massas m, como mostrado na figura abaixo, presos um ao outro por uma mola cuja força de restauração é proporcional à distância entre os dois pêndulos, (x₁-x₂), onde x₁ e x₂ são, respectivamente as posições dos pêndulos 1 e 2 da figura. As equações da dinâmica (2ª. lei de Newton) desses pêndulos são

, (9)

onde, novamente, aproximamos (lembre que os ângulos de abertura são pequenos) x₁=lq₁ e x₂=lq₂.

A equação (6) era mais simples. Agora a situação complicou, pois precisamos achar as soluções para q₁ e q₂ em função do tempo e essas duas variáveis aparecem nas duas equações. O nome técnico disso é: equações diferenciais acopladas. Para resolver essas equações há um truque em dois passos: primeiro, somamos e subtraímos as duas equações acima. Fazendo isso ficamos com

. (10)

Agora, segundo passo do truque, vamos chamar de X e de Y. Com esses novos nomes as equações acima ficam

. (11)

Cada uma dessas equações tem a “cara” da equação (6). Portanto, as soluções são

, (12)

onde e . Mas o que queremos é e e não X e Y. Como e , então e . Usando X e Y das equações (12) temos,

. (13)

O problema inicial era descobrir como andar com as pernas amarradas por um elástico ou uma mola. Será que fomos longe demais com a matemática e perdemos nosso foco? Não, apenas precisamos interpretar essas duas equações acima. Um movimento geral das duas pernas é descrito pelas equações (13), escolhendo adequadamente B₁, B₂, f₁ e f₂ de acordo com algumas condições do problema, por exemplo, as condições de posição e velocidade dos dois pêndulos em t=0. Entretanto, não queremos exatamente uma solução geral. O que queremos é descobrir valores de B₁ e B₂ que nos permita andar com nossas próprias pernas Quando andamos, as duas pernas oscilam fora de fase, ou seja, uma vai para frente e outra para trás. Assim, os termos em B₁ não nos importam, pois eles correspondem a um balançar das duas pernas em fase: ambas vão juntas para frente e para trás. A solução que serve para andar é aquela que depende de B₂:

, (14)

onde B₂ é o tamanho de um passo. Portanto, o modo normal de andar têm uma freqüência angular e a freqüência dada pela equação (3).

---

[1] Uma aproximação melhor seria considerar a perna um pêndulo físico uniforme, o que mudaria o período por um fator .