Uma força interessante

Forças e forças

         Há, na Natureza, quatro forças chamadas de fundamentais. Uma delas é bem familiar, a força gravitacional. Ela é responsável pela nossa sensação de peso, pelo movimento de rotação da Terra em torno do Sol e da Lua em torno da Terra.

Outra, a força eletromagnética, é também bem conhecida, pelo menos por aqueles que prestaram atenção às aulas do ensino médio. Esta força é a responsável pela estrutura de átomos e moléculas e também está presente nos equipamentos e instrumentos elétricos e eletrônicos.

Existem duas outras forças que não conseguimos perceber no nosso dia-a-dia, mas que são muito importantes. Elas se manifestam em especial nos núcleos atômicos, nas interações entre seus constituintes e entre os constituintes de seus constituintes. Estas forças são as responsáveis pela estabilidade ou instabilidade dos núcleos e das partículas elementares.

Forças no dia-a-dia

         No dia-a-dia, as forças que encontramos têm origem nas interações fundamentais da Natureza. Por exemplo, a força de atrito é provocada pela interação eletromagnética entre os átomos ou moléculas das superfícies em contacto. O peso das coisas é provocado pela atração gravitacional. A interação eletromagnética é responsável pelos raios.

         Entretanto, muitas das forças que encontramos podem ser entendidas e explicadas sem a necessidade de se fazer referência às forças fundamentais. Por exemplo, a força de resistência do ar que sentimos quando pedalamos em alta velocidade, ou a força que “segura” um carro a alta velocidade, é provocada pelo fato que um objeto que se desloca precisa empurrar o ar à sua frente. E quanto mais rapidamente o objeto se desloca, mais rapidamente precisa empurrar o ar e mais empurra em cada intervalo de tempo. Embora a interação do ciclista ou do carro com cada molécula do ar seja do tipo eletromagnética, podemos explicar a força de arrasto, como é chamada a força que segura ciclistas e carros, sem fazer referência à força eletromagnética.

         Outra força que tem origem na força eletromagnética, mas que explicamos e entendemos sem fazer referência a ela, é a força que uma mola comprimida ou esticada faz no sentido de voltar para a posição relaxada. Se esticamos ou comprimimos uma mola, cada um de seus átomos ou moléculas é ligeiramente afastado ou aproximado de seus vizinhos. Esse pequeno afastamento ou aproximação de átomos e moléculas dá origem a uma força que é percebida na mola como um todo. Essa manifestação coletiva das muitas pequenas interações entre átomos e moléculas pode ser descrita de uma forma simplificada. Em muitos casos, a força resultante da compressão ou do alongamento da mola é proporcional ao deslocamento de seu extremo em relação à posição relaxada e sempre no sentido de voltar à esta posição. Escrevendo isso na forma de uma equação,

   (1).

Nesta equação, K é uma característica da mola (mede o quão dura ela é) e x é o deslocamento em relação à posição em que a mola está relaxada, sendo chamado de elongação. O sinal de menos é para deixar claro que a força F_x é sempre no sentido oposto à elongação x.

         A figura 1 ilustra a situação. A posição marcada com um “0” na figura 1 é a posição na qual estaria o extremo da mola se ela estivesse relaxada; se o extremo dela foi “puxado” até a posição “x”, então ela fará uma força para a esquerda, igual ao produto da constante elástica da mola, K, pela elongação x. Se a mola tivesse sido comprimida, a força seria para a direita e proporcional à compressão.

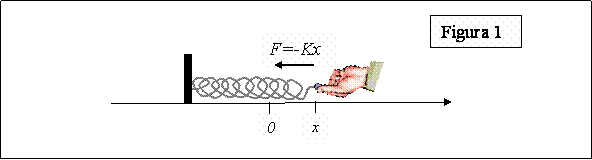
Uma força interessante

         O fato que a força exercida por uma mola é proporcional a sua elongação é bastante interessante. Por exemplo, uma mola pode ser usada como balança, pendurando-se nela o que se quer “pesar”.

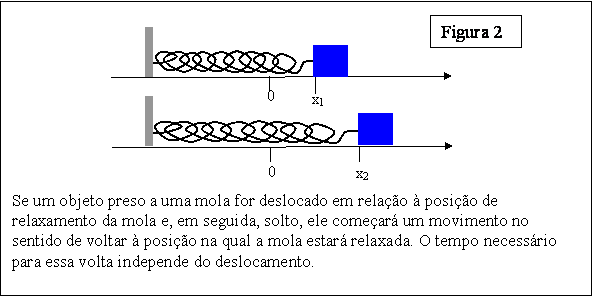
         Mas há um outro aspecto também muito interessante. Se fixarmos ao extremo de uma mola uma massa e a deslocarmos, esticando ou comprimindo a mola, o tempo que a massa levará para voltar à posição em que a mola estará relaxada independe de quanto esticamos ou comprimimos a mola. Veja a figura 2.

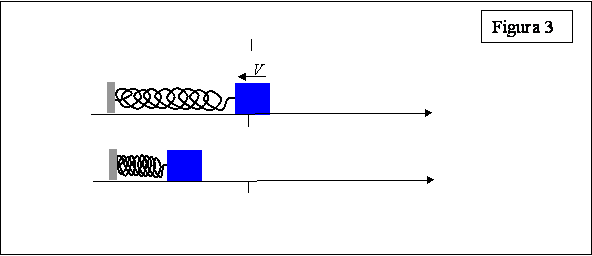
         Um aspecto importante a se considerar é que ao se esticar a mola e soltá-la em seguida, a massa irá, aceleradamente, até a posição de equilíbrio; ao passar por esse ponto, a massa começará a comprimir a mola e, portanto, ser desacelerada, até parar (veja figura 3). Depois de parar, ela começará a voltar para a posição de equilíbrio, passará por ela e voltará à posição original. Se o atrito for pequeno, esse movimento se repetirá muitas vezes: a massa oscilará entre as duas posições extremas.

O tempo de oscilação não depende de quanto comprimimos ou esticamos a mola

         Vamos provar o que está no título desta seção. Para isso, vamos fazer referência à figura 4. Na parte superior da figura (que vamos chamar de “1”) está desenhada uma massa deslocada de uma distância L em relação à posição de equilíbrio (aquela na qual a mola está relaxada, indicada pela linha tracejada). Esta massa está inicialmente parada. Então, sob a ação da força F exercida pela mola (que não está desenhada para não carregar demais a figura) ela começará um movimento acelerado para a esquerda da figura. Vamos chamar de a₁ essa aceleração. Em um pequeno intervalo de tempo Dt, a massa irá sofrer um pequeno deslocamento Dx₁. Se esse intervalo de tempo for pequeno, essa distância Dx₁ será dada por . Após esse intervalo de tempo, ela terá adquirido uma velocidade v₁ dada por . Após o intervalo de tempo Dt, a massa passará da situação A para a situação B representada na figura 4.

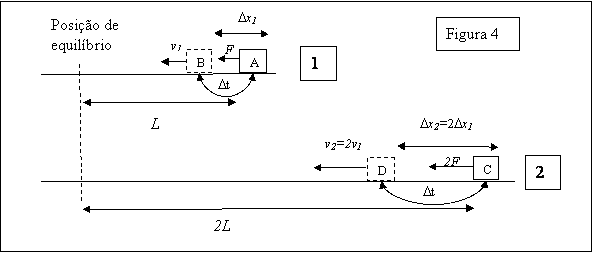
         Na parte inferior da figura (parte “2”) está desenhada uma massa idêntica, fixada à uma mola idêntica, mas deslocada de uma distância 2L da posição de equilíbrio. Assim, no instante inicial, a força sobre a massa será duas vezes maior que a força sobre a massa no caso 1; da mesma forma, a aceleração será duas vezes maior: a₂=2a₁. Portanto, no mesmo intervalo de tempo a massa do caso 2 percorrerá uma distância dada por . Mas como a₂=2a₁, então Dx₂=2Dx₁. A velocidade adquirida pela massa será por . Novamente, como a₂=2a₁, a velocidade do objeto após o pequeno intervalo de tempo será o dobro da velocidade no caso 1: v₂=2v₁. Assim, após o intervalo de tempo Dt, a massa passará da situação C para a situação D representada na figura 4.

         Fazendo um resumo, temos

   .

         Vamos examinar, agora, o que ocorrerá em um próximo intervalo de tempo Dt. Nesse novo intervalo de tempo, a massa da parte 2 da figura iniciará o movimento com uma aceleração duas vezes maior – pois ainda está duas vezes mais distante da posição de equilíbrio – e com uma velocidade também duas vezes maior que a massa da parte 1 Vamos chamar de  e  as acelerações das duas massas no início deste novo intervalo de tempo. Assim, decorrido um novo intervalo de tempo Dt, elas terão percorrido distâncias

   .

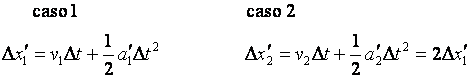Após esse novo intervalo de tempo, as velocidades serão

   .

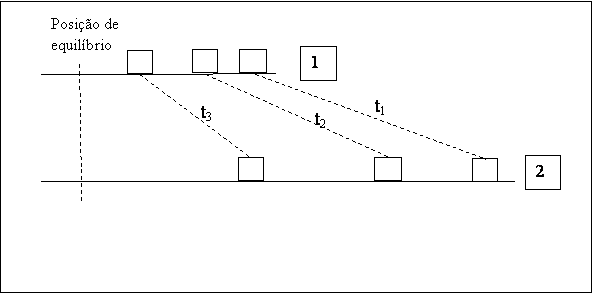
         Novamente, vemos que a massa da parte 2 da figura terá percorrido uma distância duas vezes maior que a massa da parte 1 e, também, terá, ao final do intervalo Dt, uma velocidade duas vezes maior. Essa situação continuará durante todo o movimento: comparada à massa da parte 1 da figura, a cada instante a massa da parte 2 terá o dobro da velocidade, sofrerá o dobro da força, terá o dobro da aceleração e percorrerá, a cada intervalo de tempo, o dobro da distância. Assim, ambas chegarão ao ponto de equilíbrio no mesmo instante. Essa situação é ilustrada pela figura 5.

Figura 5 – Em qualquer instante de tempo, a massa da parte 2 da figura terá, em comparação à massa da parte 1, o dobro da velocidade, o dobro da aceleração e, também, a cada intervalo de tempo percorrerá o dobro da distância. Ambas chegarão no ponto de equilíbrio no mesmo instante.

         Esse efeito continuará: elas pararão no mesmo instante, começarão o percurso de volta também no mesmo instante, chegarão novamente à posição inicial no mesmo instante, etc. A conseqüência disso é que ambas oscilarão com a mesma freqüência. Conclusão: a freqüência de oscilação não depende da amplitude do movimento.

         Embota tenhamos suposto que a massa da parte 2 da figura tenha sido deslocada, inicialmente, duas vezes mais que a massa da parte 1, as conclusões são válidas para qualquer outra proporção entre os deslocamentos iniciais.

Qual é a freqüência de oscilação?

         Os argumentos acima permitiram concluir que uma massa presa a uma mola oscilará com uma freqüência e, portanto, com um período que não depende da amplitude de oscilação. Mas, qual é essa freqüência e esse período?

         Uma maneira de descobrir isso é comparar a oscilação com o movimento circular uniforme. Considere uma massa girando uniformemente em um círculo de raio R como mostrado na figura 6.

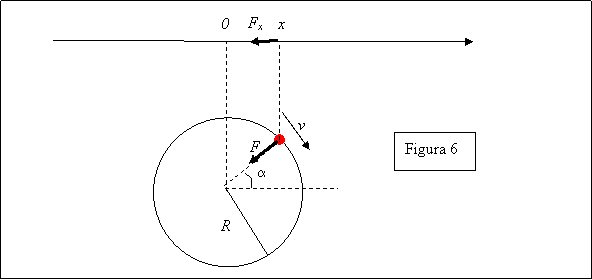
         Vamos escrever a equação que relaciona a velocidade no movimento circular uniforme com a força centrípeta:

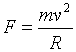   .   (2)

Agora, vamos ver como fica o movimento circular uniforme quando projetado em um eixo, representado na figura 6. A força será

   .   (3)

Mas, a projeção da posição do objeto, x (veja a figura), é . Portanto, . Se substituirmos esta igualdade na equação (3), obtemos

   .   (4)

Se usarmos a equação (2), podemos reescrever a equação (4) na forma

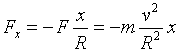   .   (5)

Compare esta equação com a equação (1), : vemos que o termo -mv²/R² na equação (5) faz o mesmo papel que K na equação (1). Ou seja, a projeção em um eixo do movimento circular uniforme de uma massa faz um movimento igual ao movimento feito por essa massa presa a uma mola de constante elástica

   .   (6)

Mas, R e v estão relacionados entre si pelo período de rotação, T. A velocidade é igual ao comprimento da circunferência dividido pelo período: v=2pR/T. Usando esta relação na equação (6), temos

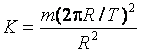   .   (7)

Finalmente, isolando T nesta última equação, obtemos

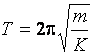   .   (8)

         Conclusão: uma massa m presa a uma mola de constante elástica K oscilará com um período T dado pela equação acima, independentemente da amplitude de oscilação.

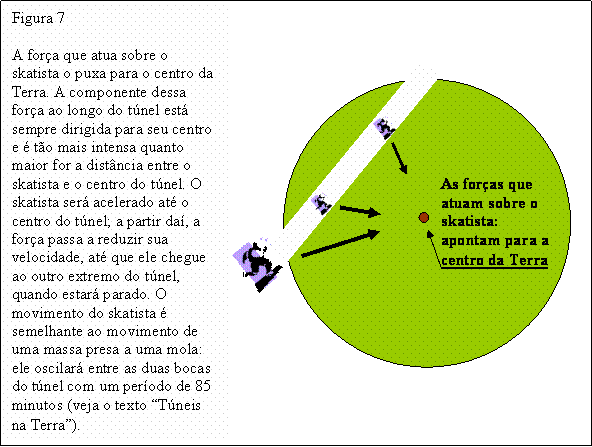
Esse resultado é usado em uma situação interessante no texto “Túneis na Terra”: construa um túnel ligando dois pontos da superfície do planeta; pegue um skate, entre nesse túnel e comece a deslizar (veja a figura 7); você chegará ao outro extremo do túnel em um tempo que independe da distância entre os dois pontos unidos pelo túnel.