Volta ao Mundo em 80 minutos

A volta ao Mundo em 80 minutos

         Como calcular o período de um satélite em órbita circular em torno da Terra? A resposta é simples: um satélite em órbita circular deve ter um período tal que a força centrípeta seja igual à força gravitacional.

         Vamos, primeiro, imaginar um satélite com uma órbita circular bastante baixa, quase na superfície da Terra, onde a aceleração gravitacional é g=9,8 m/s². Neste caso a força gravitacional (força peso) é

   ,    (1)

onde m é a massa do satélite e g a aceleração gravitacional. A força centrípeta necessária para que o satélite descreva uma órbita de raio r com velocidade v é

   .   (2)

Igualando essas forças, temos

   .   (3)

Se a órbita é bem baixa, então r é o raio da Terra, r=6.400 km. A velocidade é, então,

   .   (4)

         Uma volta inteira na Terra corresponde a uma distância 2πr~40.000 km. Portanto, este satélite demorará 1,41 h para dar uma volta completa na Terra, ou 1h25’, ou, ainda, 85 minutos: “um pouco” mais rápido que o balão do romance de Julio Verne, que demorou 80 dias para dar a volta ao Mundo.

Órbitas baixas

Alguns satélites, os geoestacionários, aqueles que permanecem o tempo todo sobre um mesmo ponto do equador terrestre, têm órbitas bem afastadas da Terra. Estes satélites são, por exemplo, os de comunicação. Mas também alguns satélites que acompanham permanentemente as condições atmosféricas de uma mesma região do planeta também são geoestacionários. Estes têm órbitas bem altas. Outros, como os meteorológicos e os militares, têm órbitas baixas.

Entretanto, os satélites de órbitas baixas não andam “raspando” na Terra. A razão para isso não é apenas para evitar bater na cabeça das pessoas, dar trombada com montanhas ou destruir arranha-céus. O problema é que próximo à superfície da Terra tem muito ar e este “seguraria” o satélite, exigindo um motor muito possante mantê-lo em órbita (satélites não têm motores).

         Os satélites orbitam a Terra a algumas centenas de quilômetros de altitude, onde a densidade da atmosfera é muito baixa, muito mesmo. Por exemplo, a Estação Espacial Internacional tem uma altitude de cerca de 360 km de altitude. Nessa altura, a densidade da atmosfera é tão baixa que o satélite pode dar milhões de voltas na Terra sem que a perda de energia seja significativa.

         Mas a 360 km de altura a aceleração da gravidade não é tão diferente da aceleração da gravidade no nível do solo. Vejamos. A força gravitacional diminui proporcionalmente ao inverso do quadrado da distância do centro da Terra, 1/r². Para saber o coeficiente de proporcionalidade, podemos fazer uma regra de três:

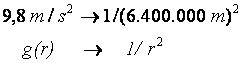      (5)

onde g(r) é a aceleração gravitacional a uma distância r do centro da Terra. Assim,

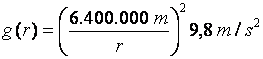   .   (6)

(Note que esta fórmula vale apenas se r for maior que 6.400 km, ou seja, um ponto fora da Terra; no interior da Terra é diferente. Sobre este assunto, veja o texto “Túneis na Terra”.)

Quando r=(6.400+360) ´10³ m obtemos g(r)=8,8 m/s². Usando uma equação análoga à equação (3), com g(r) no lugar de g, e (6.400+360)´10³ m no lugar de r, obtemos

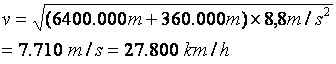   .   (7)

         Uma volta na Terra a uma altura de 6.760 km corresponde a uma distância de 42.500 km. A 27.800 km/h, uma volta completa na Terra demorará 1,53 h ou 1h32’ ou, ainda, 92 minutos, não muito diferente do período de um satélite a baixíssima altitude. Esse é o período da órbita dos satélites de observação e, também, da Estação Espacial Internacional.

         A possibilidade de viagens por satélites poderia ser interessante. Iríamos daqui ao Japão em pouco mais do que meia hora. Entretanto, isso não seria nem economicamente viável, nem ecologicamente correto. Numa viagem de avião daqui até o Japão, o consumo de combustível por passageiro é de algumas centenas de litros (boa parte do custo das passagens aéreas vem do combustível). Para acelerar uma espaçonave até uma velocidade de 7.700 km/h precisaríamos gastar alguns milhares de litros de combustível por passageiro (supondo que a quantidade de “lata” por passageiro em um avião e em uma espaçonave pudessem ser iguais). Assim, a viagem se tornaria muito cara e ecologicamente incorreta. Para uma maneira igualmente rápida de se viajar de um ponto a outro da Terra – e sem consumo de combustível –, veja o texto “Túneis na Terra”.

Satélites estacionários

         Alguns satélites ficam parados sobre um mesmo ponto no equador: se alguém que está na linha do equador, bem abaixo da órbita de um desses satélites estacionários, olhar para o céu, com a ajuda de uma luneta, verá um objeto “parado” o tempo todo sobre sua cabeça. Provavelmente, acharia muito estranho: afinal, por que aquela coisa, aparentemente parada no céu, não cai? Se essa pessoa souber Física entenderá que a Terra e o satélite estão, ambos, girando com a mesma velocidade angular. Se não souber Física, ficará admirada ao ver um objeto parado no céu e que se nega a cair.

Para estudar o caso de satélites estacionários, vamos, novamente, trabalhar com as equações (1) e (2), que devem ser iguais. Mas se a órbita é estacionária, então o período de rotação do satélite, T, é de 24 h. Portanto, há uma relação adicional entre a velocidade e a posição do satélite, v e r: T=. Para não haver chance de confusão com as unidades, vamos escrever essa equação no Sistema Internacional: T=. Usando a relação , as equações (1) e (2) e considerando a expressão (6) para a aceleração gravitacional em função da altitude, obtemos a altura (medida em relação ao centro da Terra) que está o satélite:

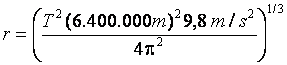   .   (8)

Fazendo as contas, obtemos r=42 mil quilômetros. Esta é a distância entre um satélite em órbita estacionária e o centro da Terra.

         De fato, os satélites estacionários, como os de comunicação e os da série Goes de observação atmosférica estão a cerca de 36 mil quilômetros da superfície da Terra. Somando-se este valor ao raio terrestre, obtemos o valor acima para a distância do satélite ao centro da Terra.

A Lua

         A Lua está a cerca de 3,8 10⁸ m de distância da Terra. Para descobrimos o seu período de rotação vamos usar a mesma equação (8), mas escrevendo T em função de r:

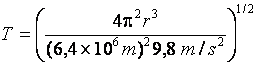   .   (9)

Fazendo as contas, descobrimos que o período de rotação da Lua é de cerca de 28 dias.